

 |
 |
В 1679 году Исаак Ньютон показал, что любое тело в поле тяготения будет двигаться по коническому сечению.
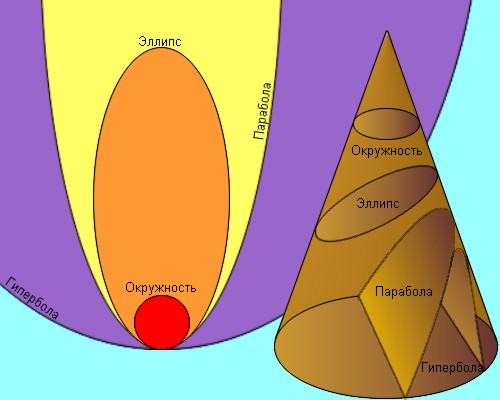 |
| Рисунок 3.1.2.1.1. Конические сечения и космические орбиты
|
Конические сечения образуются при пересечении прямого кругового конуса с плоскостью. К коническим сечениям относятся кривые второго порядка: эллипс, парабола и гипербола, а также пара параллельных прямых. Все они является геометрическим местом точек, отношение расстояний от которых до заданной точки (фокуса) и до заданной прямой (директрисы) есть величина постоянная, равная эксцентриситету
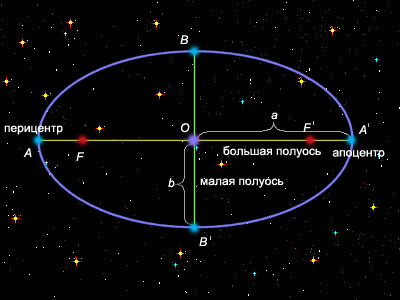 |
| Рисунок 3.1.2.1.2. Важнейшие точки и линии эллипса
|
Эллипс определяется как геометрическое место точек, для которых сумма расстояний от двух заданных точек (фокусов
Большая полуось
Она связана с механической энергией тела следующим соотношением
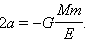 |
Так как при движении по эллипсу полная энергия отрицательна, большая полуось больше нуля. Длина малой полуоси
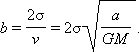 |
Круговые орбиты являются вырожденным случаем эллиптических. Записывая второй закон Ньютона, получим, что кинетическая и потенциальная энергия тела на круговой орбите связаны соотношением:
|
2 |
Применяя закон сохранения энергии, легко получить, что
Элементы орбиты характеризуют форму, размеры и ориентацию в пространстве орбиты небесного тела, а также положение тела на этой орбите. В настоящее время для описания положения планеты или спутника широко используются оскуллирующие элементы.
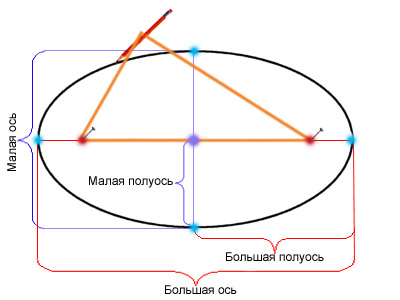 |
| Рисунок 3.1.2.1.3. Как нарисовать эллипс?
|
Точка орбиты тела, ближайшая к притягивающему центру (фокусу), в общем случае называется перицентром, а наиболее удаленная от него (только у эллипса) – апоцентром. Если притягивающим центром является Земля, то эти точки называются соответственно перигеем и апогеем. Наиболее близкая точка к Солнцу называется перигелий, наиболее удаленная – афелий. Для Луны эти точки будут перилунием (периселением) и аполунием (апоселением), для произвольной звезды – периастром и апоастром. Прямая, соединяющая перицентр с фокусом (большая ось эллипса, ось параболы или действительная ось гиперболы), называется линией апсид.
Расстояние от притягивающего центра до перицентра равно
 |
 |
 |

