

 |
 |
Три закона движения планет относительно Солнца были выведены эмпирически немецким астрономом Иоганном Кеплером в начале XVII века. Это стало возможным благодаря многолетним наблюдениям датского астронома Тихо Браге.

 |
|
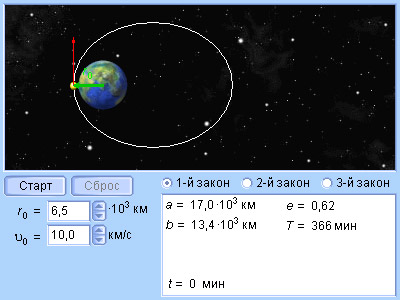
Модель 3.3.
Законы Кеплера
|
Современная формулировка первого закона дополнена так: в невозмущенном движении орбита движущегося тела есть кривая второго порядка – эллипс, парабола или гипербола.
В отличие от двух первых, третий закон Кеплера применим только к эллиптическим орбитам.
Скорость движения планеты в перигелии
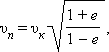 |
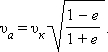 |
Кеплер открыл свои законы эмпирическим путем. Ньютон вывел законы Кеплера из закона всемирного тяготения. Для определения масс небесных тел важное значение имеет обобщение Ньютоном третьего закона Кеплера на любые системы обращающихся тел.
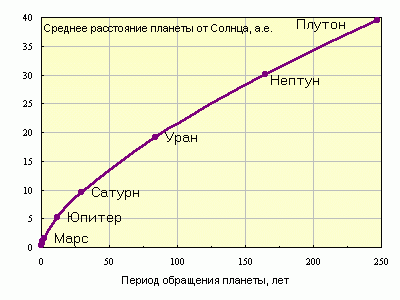 |
| Рисунок 3.1.3.1. Третий закон Кеплера. Скорости близких к Солнцу планет значительно больше, чем скорости далеких
|
В обобщенном виде этот закон обычно формулируется так: квадраты периодов ![]() )
)
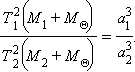 |
При этом взаимодействие между телами ![]()
![]()
|
Третий закон Кеплера можно также выразить как зависимость между периодом
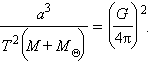 |
Здесь необходимо сделать следующее замечание. Для простоты часто говорится, что одно тело обращается вокруг другого, но это справедливо только для случая, когда масса первого тела пренебрежимо мала по сравнению с массой второго (притягивающего центра). Если же массы сравнимы, то следует учитывать и влияние менее массивного тела на более массивное. В системе координат с началом в центре масс орбиты обоих тел будут коническими сечениями, лежащими в одной плоскости и с фокусами в центре масс, с одинаковым эксцентриситетом. Различие будет только в линейных размерах орбит (если тела разной массы). В любой момент времени центр масс будет лежать на прямой, соединяющей центры тел, а расстояния до центра масс
Третий закон Кеплера можно использовать, чтобы определить массу двойных звезд.
 |
 |
 |

