Математика. Сфера и шар. Касания и сечения

Тема. Круглые тела. Сфера и шар. Сечение шара плоскостью.

Автор: Андреева Е.И.

Тип урока. Урок изучения нового учебного материала.

Цель урока. Сформировать у учащихся представления о сфере и шаре, рассмотреть случаи их взаимного расположения с плоскостью.

Задачи урока:

• формирование и развитие у учащихся пространственного воображения;
• систематизация материала в виде обзорной лекции;
• совершенствование умения анализировать, обобщать, доказывать новое;
• развитие коммуникативных навыков учащихся.

Основные понятия. Круглые тела. Сфера Шар. Сечение шара плоскостью. Центр сферы (шара). Радиус сферы (шара). Хорда сферы (шара). Диаметр. Большая окружность сферы. Большой круг шара. Касательная прямая. Касательная плоскость.

Мировоззренческий аспект урока. Развитие навыков логического мышления и научного подхода к изучению мира у учащихся.

Использование новых информационных технологий: Использование интерактивной доски и интерактивных моделей курса серии «Открытая коллекция» «Математика: стереометрия, 10–11 классы» (Windows, Linux)

План урока

I. Этап актуализации знаний. Мотивация учебной проблемы

1. Какие тела называются круглыми?

2. Какие круглые тела вы знаете?

3. Каким образом можно получить круглые тела?

II. Изучение нового материала. Формирование у учащихся представлений о сфере, шаре, взаимных расположений сферы и плоскости

Важным классом фигур в пространстве, помимо многогранников, является класс фигур, называемых фигурами или телами вращения.

Сфера получается вращением окружности вокруг её диаметра. Аналогично, шар получается вращением круга вокруг какого-нибудь его диаметра.

Демонстрация на интерактивной доске иллюстрации «Методика получения сферы».

Множество всех точек пространства, одинаково удалённых на расстояние R от данной точки O, называется сферой.

Демонстрация интерактивного графика «Радиус сферы»:

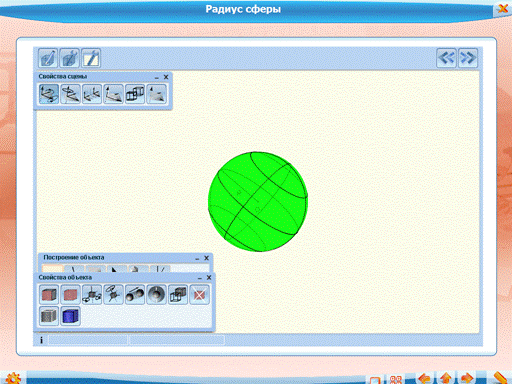
Сферу обозначают так: ω (O, R). Можно определить сферу и как тело, образованное при вращении окружности вокруг своего диаметра.

Демонстрация иллюстрации «Образующий полукруг шара».

Множество всех точек пространства, удалённых от данной точки O на расстояние, не большее R, называется шаром.

Иными словами шар – это объединение сферы и всех её внутренних точек.

Можно также определить шар и как тело, образованное при вращении круга вокруг своего диаметра.

Шар обозначают так же, как сферу: ω (O, R). Точка O называется центром сферы (шара). Отрезок, соединяющий центр сферы с любой её точкой, называется радиусом сферы (шара). Отрезок, соединяющий любые две точки сферы, называется хордой сферы (шара). Иногда под радиусом или хордой подразумевают их длину. Хорда, проходящая через центр сферы, называется её диаметром.

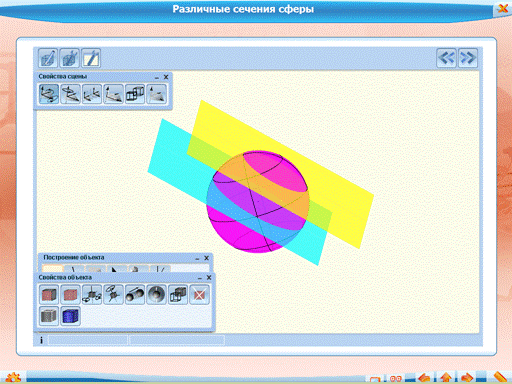
При пересечении сферы плоскостью наибольшая окружность образуется, если плоскость проходит через центр сферы. Линия пересечения называется большой окружностью сферы. Соответствующее сечение шара называется большим кругом шара.

При объяснении этих понятий можно продемонстрировать иллюстрацию «Сфера и шаровой сектор»:

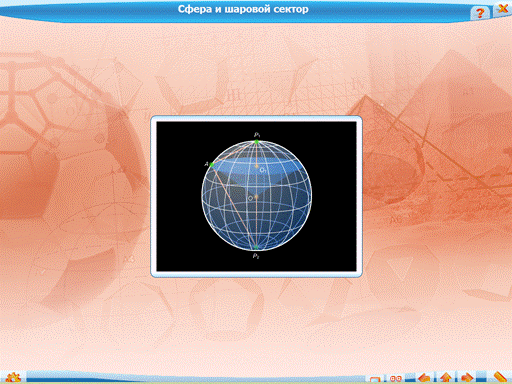
и интерактивную модель «Сфера и ее элементы»:

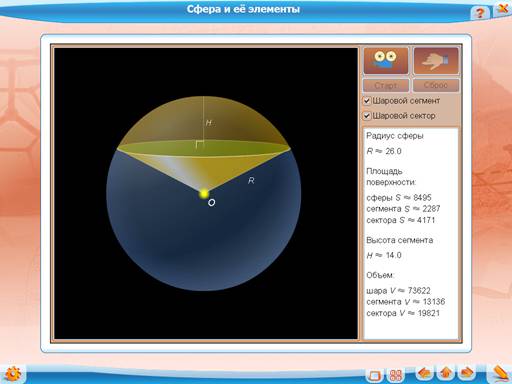
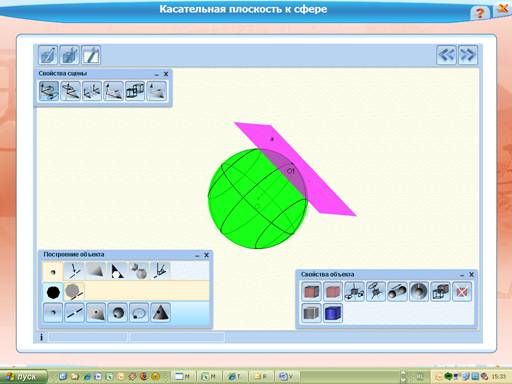
Касательной плоскостью к сфере называется плоскость, имеющая единственную общую точку со сферой.

Теорема. Если расстояние от центра сферы до плоскости меньше радиуса сферы, то линия сечения сферы этой плоскостью – окружность.

Из теоремы следует, что, когда расстояние от центра шара до плоскости меньше радиуса, то сечение шара этой плоскостью – круг. Если плоскость удалена от центра сферы на расстояние R, то она является касательной плоскостью.

При объяснении теоремы и вводе новых понятий можно показать иллюстрацию «Шаровой сегмент»:

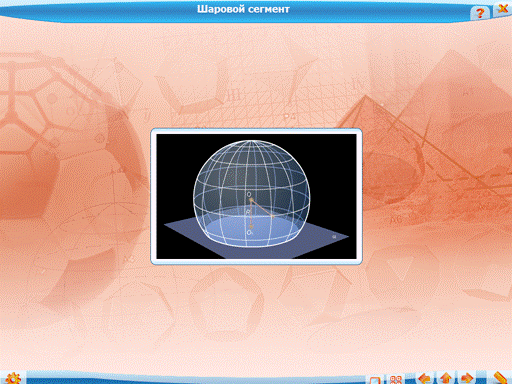
Интерактивный график о различных сечениях сферы:

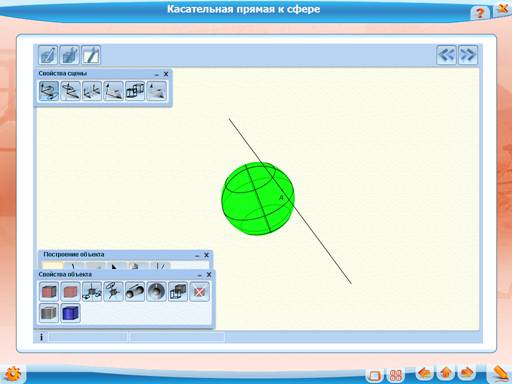
Касательная прямая сферы имеет со сферой единственную общую точку.

Через любую точку сферы можно провести бесконечное число касательных прямых, причем все они лежат в касательной плоскости.

Прямая, касающаяся сферы – это прямая, которая имеет единственную общую точку со сферой.

Интерактивный чертеж «Касательная прямая к сфере»:

Интерактивный чертеж «Касательная плоскость к сфере»:

Аналогично можно ввести понятие касательной прямой к поверхности конуса (цилиндра), однако при этом рассматриваются прямые, не проходящие через точки на основании конуса (цилиндра) и через вершину конуса.

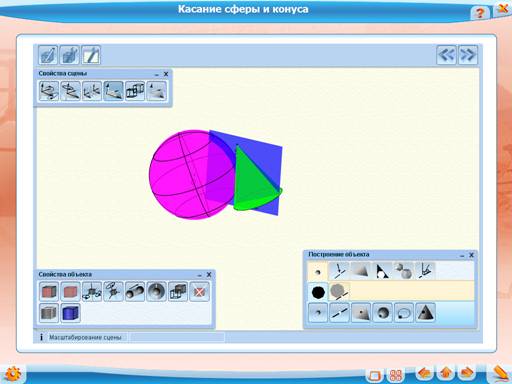
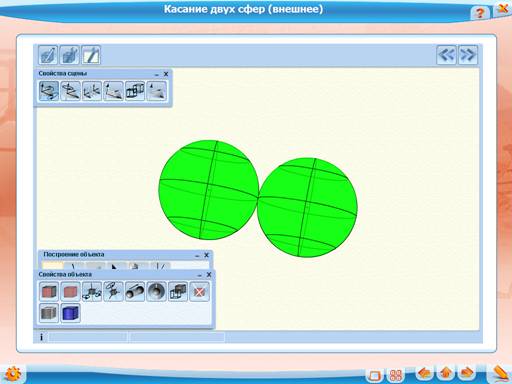
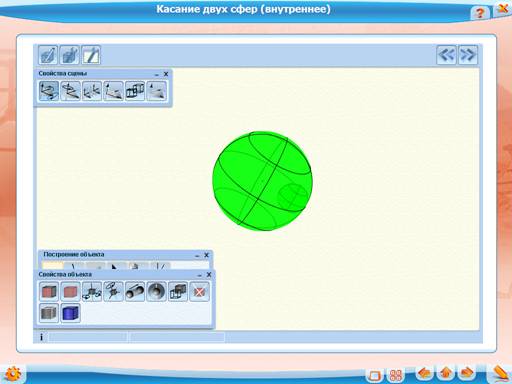
Так же несложно определяются понятия двух касающихся сфер и сферы, касающейся боковой поверхности конуса. Однако при решении задач, в которых фигурируют эти объекты, нужно быть предельно внимательным, поскольку существует два вида касания: внутреннее и внешнее.

Демонстрация интерактивных чертежей «Касание двух сфер (внешнее)» и «Касание двух сфер (внутреннее)».

III. Решение задач

Третью часть занятия рекомендуется провести с активным решением задач как учащимися у интерактивной доски, так и проведением фронтальной беседы с учащимися. Это поможет активизации внимания учащихся. Для этих целей рекомендуется использовать 3–5 интерактивных заданий, подобранных из темы «5.3. Сфера». В качестве примера приведём ряд задач.

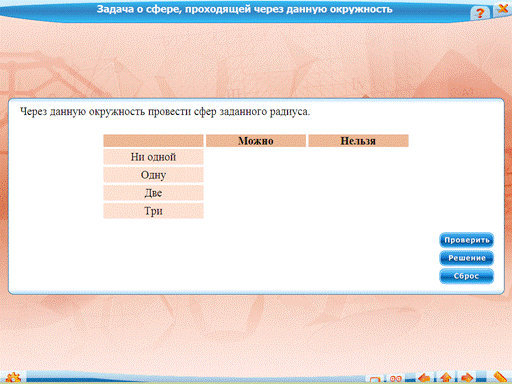
Задача о сфере, проходящей через данную окружность:

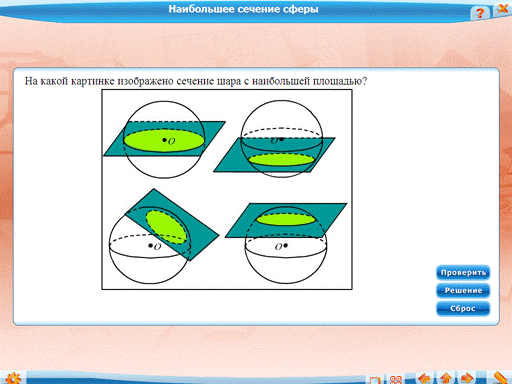
Задача о наибольшем сечениии сферы:

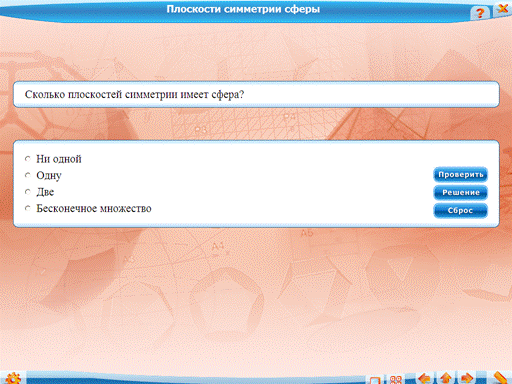
Задача о плоскости симметрии сферы:

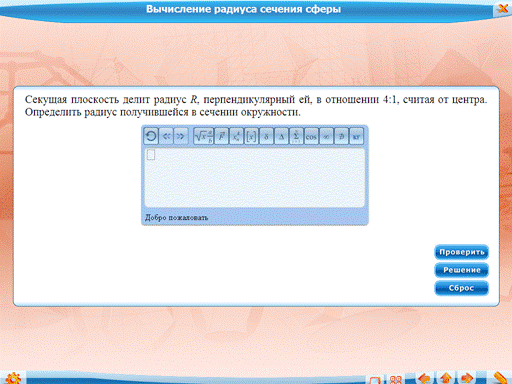
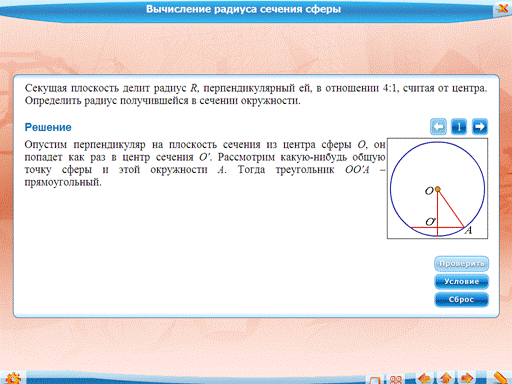
Задача о нахождении радиуса сечения сферы:

IV. Первичная проверка усвоения знаний. Рефлексия

Проверка усвоения знаний по теме проводится с использованием устных заданий в виде блиц-опроса.

1. Сколько сфер можно провести: а) через одну и ту же окружность; б) через окружность и точку, не принадлежащую её плоскости?
(а) бесконечно много; б) одну).

2. Сколько сфер можно провести через четыре точки, являющиеся вершинами: а) квадрата; б) равнобедренной трапеции; в) ромба?
(а) бесконечно много; б) бесконечно много; в) ни одной).

3. Верно ли, что через любые две точки сферы проходит один большой круг?
(Нет).

4. Через какие две точки сферы можно провести несколько окружностей большого круга?
(Диаметрально противоположные).

5. Как должны быть расположены две равные окружности, чтобы через них могла пройти сфера того же радиуса?
(Иметь общий центр).

V. Домашнее задание

Решить задачи:

1. Шар с центром в точке О касается плоскости. Точка А лежит в этой плоскости. Найдите расстояние от точки А до точки касания, если её расстояние от центра шара равно 25 см, а радиус шара равен 15 см.

2. В шаре радиуса 26 см на расстоянии 10 см от центра проведена секущая плоскость. Найдите плоскость сечения.

Помимо предложенных задач рекомендуется выдать учащимся на дом и задания из учебника.