Квадратичная функция и ее график

Тема. Квадратичная функция и ее график

Автор: Андреева Е.И.

Тип урока. Изучение нового материала

Цель урока. Учащиеся должны научиться строить графики квадратичной функции,

Основные понятия. График квадратичной функции.

Использование новых информационных технологий: Использование интерактивной доски и интерактивных моделей курса серии «Открытая коллекция» «Математика: алгебра, 7–11 классы» (Windows, Linux)

План урока

I. Этап актуализации знаний

1. Какое уравнение называется квадратным?

2. Как определить корни квадратного уравнения?

3. Всегда ли квадратное уравнение имеет корни?

4. Какая функция является квадратичной?

II. Изучение нового материала

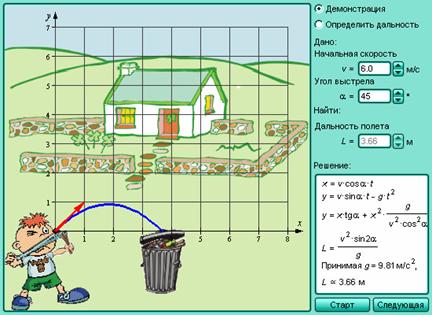
График квадратичной функции при 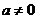называется параболой.

Можно показать модель движения по параболе, задав значение начальной скорости и угла выстрела

Рассмотрим сначала функцию

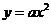
Областью определения этой функции являются любые значения .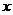

Решив уравнение

, 

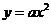получим 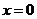. Итак, единственный нуль этой функции 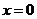. Функция является четной.

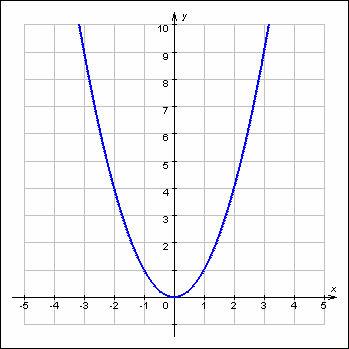
Этот рисунок рекомендуется вывести на интерактивную доску.

При 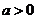функция убывает на 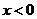и возрастает на 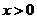. Точка 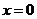является минимумом функции. Областью значений функции в этом случае является промежуток .

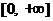При 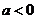функция возрастает на 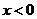и убывает на 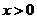. Точка 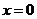является максимумом функции. Областью значений функции в этом случае является промежуток .

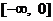График функции 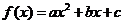легко построить из графика функции 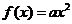геометрическими преобразованиями, используя формулу

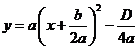
Для этого нужно растянуть график 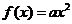в 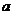раз от оси OX, при необходимости отразив его относительно оси абсцисс, а затем сместить получившийся график на 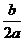влево и на 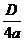вниз (если какое-либо из этих чисел меньше нуля, то соответствующее смещение нужно производить в противоположную сторону).

III. Работа на интерактивной доске с моделью квадратичной функции

Интерактивная модель демонстрирует построение произвольной параболы из графика функции 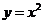методом выделения полного квадрата. Задайте квадратичную функцию вида 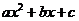(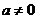) в поле ввода в нижней части модели. Рядом появится разложение трехчлена с выделением полного квадрата.

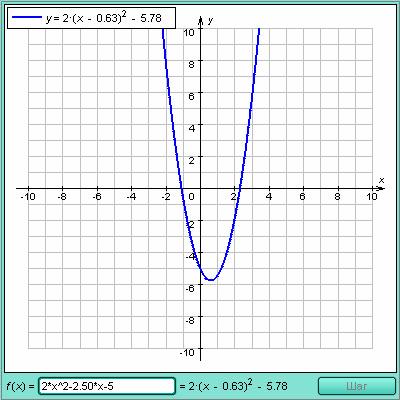
Учащимся предлагается задание построить график квадратичной функции. Задание предлагается в двух вариантах. На доске это задание выполняют два ученика, а остальные делают это у себя в тетрадях.

После его выполнения учитель предлагает проверить построенные графики с помощью интерактивной модели

IV. Рефлексия. Формирование умений и навыков.

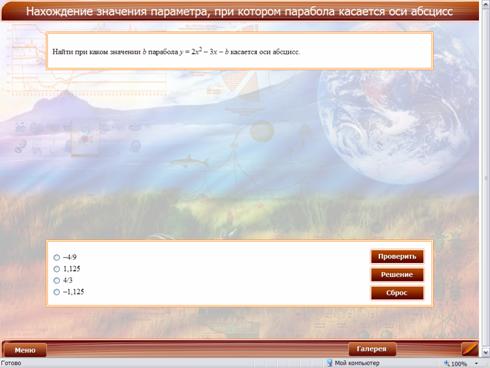
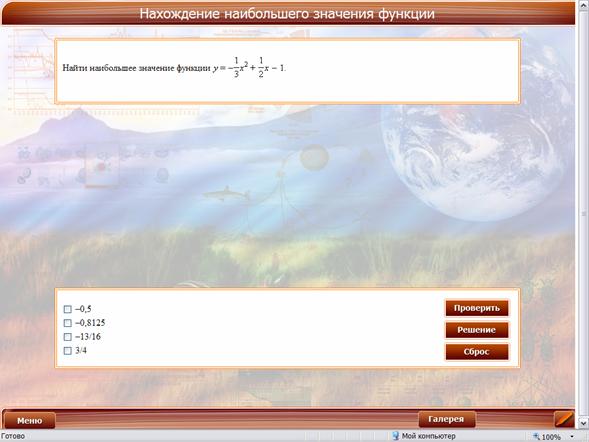
Тестовые задания рекомендуется спроектировать на интерактивную доску, чтобы задание было видно всему классу. Опрос проводить фронтально, объясняя сложные вопросы.

Общий вид тестовых заданий виден на рисунке. В некоторых заданиях верными могут являться несколько дистракторов.

1. Найти при каком значении b парабола 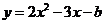касается оси абсцисс.

а. 4/3

Комментарий. Парабола касается оси, значит, вершина параболы лежит на оси, дискриминант равен 0. .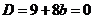

б. 1,125

Комментарий. Парабола касается оси, значит, вершина параболы лежит на оси, дискриминант равен 0. .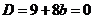

в. –1,125

г. –4/9

Комментарий. Парабола касается оси, значит, вершина параболы лежит на оси, дискриминант равен 0. .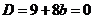

Верный ответ 3.

2. Найти наибольшее значение функции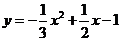

а.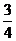

Комментарий. Найдена абсцисса вершины параболы, необходимо вычислить ординату

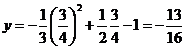
б. –0,5

Комментарий. Найти координаты вершины параболы затем вычислить ординату

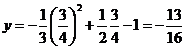
в. –13/16

г. –0,8125

Верный ответ: 3, 4

V. Домашнее задание

Список квадратичных функций для построения дома графиков, теоретический материал урока.